リスト型
リストの作成:変数名 = [1, 2, 3, ...]
リスト同士の演算
リスト同士を足し算すると、リストが連結される
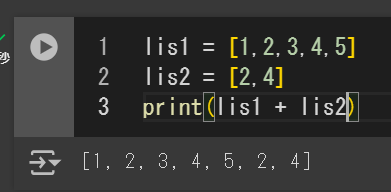
リスト同士の引き算、掛け算、割り算はエラーになる
リストに対する演算
リストに整数を掛けると、その整数の回数分リピートされる

足し算、引き算、割り算はエラーになる
リストを引き算したい場合
・引きたい要素を引いた新しいリストを作ることで実現する
・リストに対してinを使うと計算量がO(N)になるが、setを使えばO(1)になるらしい
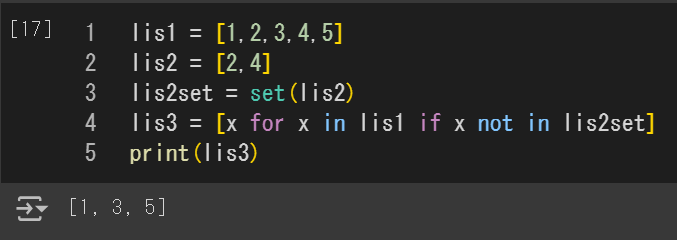
リストの各要素に演算したい場合:map()
・map()を使うことで、リストの各要素に好きな関数を適用できる(forループと同じ)
・mapの第一引数に直接ラムダを書くのもOK
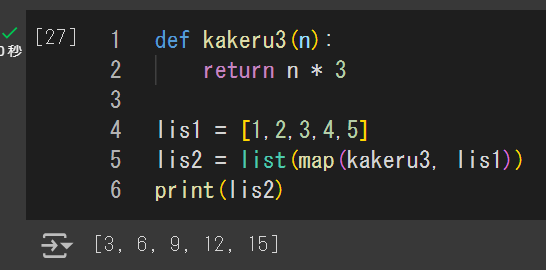
↑をforループで書いた場合
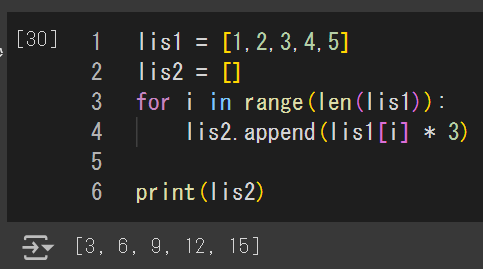
リストをフィルターしたい場合
・内包表記とfilter関数のどちらでも実現可能
内包表記:条件文をその場で書く

filter関数:あらかじめ関数を定義し、それをリストに適用する(map()と似てる)
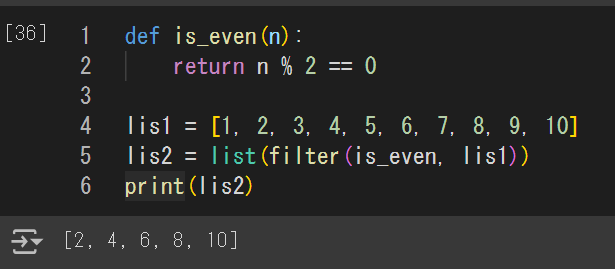
filter関数は必要か?
・パフォーマンスは内包表記とfilter関数どちらも同じくらい
・上記の内包表記はその場で定義したフィルタを他で使い回せないのが弱点
・例えばあるフィルタを20箇所で使ってて仕様変更で修正が必要になった場合、上記の内包表記の場合だと20箇所を手作業で修正する必要があり面倒
・フィルター関数なら予め定義しておいた関数を修正するだけなので1箇所の修正だけで済む
・とはいえ内包表記でも関数は使えるので、再利用性はfilter関数の専売特許というわけではない
・つまり内包表記でも事前に定義した関数を使うようにすれば、filterと同程度の再利用性を実現できる
結論:無理してfilter()を使う理由はない(関数型プログラミングをやりたいなら使う、程度か)
内包表記+関数の例

スタックとキュー
・スタック:LIFO(Last In First Out)→最後に追加された要素を最初に取り出す
例えるなら、列の後ろにいる人から恐竜に食われるイメージ
・キュー:FIFO(First In First Out)→最初に追加された要素を最初に取り出す
例えるなら、列の先頭にいる人からアイドルと握手するイメージ
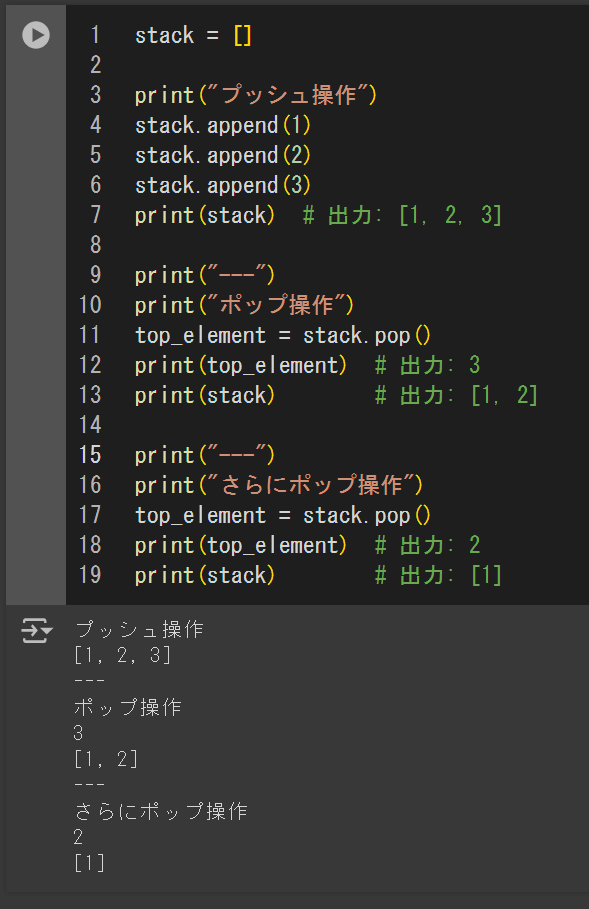
リストをスタックとして使用する方法
・プッシュ操作(要素の追加)はappend()
・ポップ操作(要素の削除)はpop()
・どちらも計算量N(1)で実行されるので速い
ChatGPT:スタックを使用するアルゴリズムの例
1. 括弧のバランスチェック
括弧のバランスが正しいかどうかを確認するアルゴリズムです。
def is_balanced(expression):
stack = []
pairs = {')': '(', '}': '{', ']': '['}
for char in expression:
if char in pairs.values():
stack.append(char)
elif char in pairs.keys():
if stack == [] or stack.pop() != pairs[char]:
return False
return stack == []
# 使用例
expression = "{[()()]}"
print(is_balanced(expression)) # 出力: True
expression = "{[(])}"
print(is_balanced(expression)) # 出力: False2. 深さ優先探索 (Depth-First Search, DFS)
グラフやツリーの探索に使用されるアルゴリズムです。
def dfs(graph, start):
visited = set()
stack = [start]
while stack:
vertex = stack.pop()
if vertex not in visited:
print(vertex, end=" ")
visited.add(vertex)
stack.extend(reversed(graph[vertex])) # 逆順に追加することで正しい順序で探索する
# 使用例
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': ['F'],
'F': []
}
dfs(graph, 'A') # 出力: A C F B E D3. 中置記法から後置記法への変換 (Shunting Yard アルゴリズム)
中置記法の数学表現を後置記法(逆ポーランド記法)に変換するアルゴリズムです。
def infix_to_postfix(expression):
precedence = {'+': 1, '-': 1, '*': 2, '/': 2, '^': 3}
stack = []
output = []
for char in expression:
if char.isalnum(): # オペランドの場合
output.append(char)
elif char == '(':
stack.append(char)
elif char == ')':
while stack and stack[-1] != '(':
output.append(stack.pop())
stack.pop()
else:
while stack and stack[-1] != '(' and precedence[char] <= precedence[stack[-1]]:
output.append(stack.pop())
stack.append(char)
while stack:
output.append(stack.pop())
return ''.join(output)
# 使用例
expression = "A*(B+C)"
print(infix_to_postfix(expression)) # 出力: ABC+*4. ハノイの塔
再帰を用いて解かれることが多いハノイの塔問題を、スタックを使用して非再帰的に実装する例です。
def iterative_hanoi(n, source, auxiliary, target):
stack = []
stack.append((n, source, auxiliary, target))
while stack:
n, source, auxiliary, target = stack.pop()
if n == 1:
print(f"Move disk 1 from {source} to {target}")
else:
stack.append((n - 1, auxiliary, source, target)) # Move n-1 disks from auxiliary to target
stack.append((1, source, auxiliary, target)) # Move the nth disk from source to target
stack.append((n - 1, source, target, auxiliary)) # Move n-1 disks from source to auxiliary
# 使用例
iterative_hanoi(3, 'A', 'B', 'C')5. 有効範囲内の最大値の計算
スタックを使って、各位置における有効範囲内の最大値を計算するアルゴリズムです。
def max_in_range(arr):
n = len(arr)
stack = []
max_range = [0] * n
for i in range(n):
while stack and arr[stack[-1]] <= arr[i]:
max_range[stack.pop()] = arr[i]
stack.append(i)
while stack:
max_range[stack.pop()] = -1
return max_range
# 使用例
arr = [4, 5, 2, 25]
print(max_in_range(arr)) # 出力: [5, 25, 25, -1]これらの例は、スタックを利用して効率的に問題を解決する典型的なアルゴリズムです。スタックのLIFO特性を活かして、データの管理や探索を行う場面で頻繁に利用されます。
キューはdequeが便利
・「デキュー」と読みたくなるが、海外プログラマーは実際は「デック」と発音してるので注意
参考動画:https://www.youtube.com/watch?v=34SNQHapJYE

ChatGPT:キューを使用するアルゴリズムの例
1. 幅優先探索(Breadth-First Search, BFS)
幅優先探索はグラフやツリーの探索アルゴリズムで、最短経路の発見などに利用されます。キューを使って、探索するノードをFIFO順に処理します。
from collections import deque
def bfs(graph, start):
visited = set()
queue = deque([start])
visited.add(start)
while queue:
vertex = queue.popleft()
print(vertex, end=" ")
for neighbor in graph[vertex]:
if neighbor not in visited:
visited.add(neighbor)
queue.append(neighbor)
# 使用例
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': ['F'],
'F': []
}
bfs(graph, 'A') # 出力: A B C D E F2. レベル順のツリー走査
二分木などのツリー構造をレベル順に走査するアルゴリズムです。各レベルのノードを順番に処理するためにキューを使用します。
from collections import deque
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def level_order_traversal(root):
if not root:
return
queue = deque([root])
while queue:
node = queue.popleft()
print(node.value, end=" ")
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
# 使用例
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.right.left = TreeNode(6)
root.right.right = TreeNode(7)
level_order_traversal(root) # 出力: 1 2 3 4 5 6 73. ジョセフス問題
ジョセフス問題は、円形に並んだ人々の中で、一定のルールに従って人を排除していく問題です。キューを使って、順番に人を処理することができます。
from collections import deque
def josephus_problem(n, k):
queue = deque(range(1, n + 1))
while len(queue) > 1:
for _ in range(k - 1):
queue.append(queue.popleft())
queue.popleft() # k番目の人を排除
return queue[0]
# 使用例
print(josephus_problem(7, 3)) # 出力: 44. プロセススケジューリング
オペレーティングシステムでのプロセススケジューリングにおいて、キューを使ってプロセスを管理し、FIFO順でプロセスを実行します。
from collections import deque
class ProcessQueue:
def __init__(self):
self.queue = deque()
def add_process(self, process):
self.queue.append(process)
def execute_process(self):
if self.queue:
process = self.queue.popleft()
print(f"Executing process: {process}")
# 使用例
pq = ProcessQueue()
pq.add_process("Process 1")
pq.add_process("Process 2")
pq.add_process("Process 3")
pq.execute_process() # 出力: Executing process: Process 1
pq.execute_process() # 出力: Executing process: Process 2
pq.execute_process() # 出力: Executing process: Process 3これらの例は、キューを利用する典型的なアルゴリズムの一部です。キューの特性であるFIFO(First In, First Out)を活かして、様々なアルゴリズムを効率的に実装することができます。